Manual

Basics

General Invocation

A01_Cube

Objects are created by the use of a Lua script. The reference manual for lua is HERE Any script just needs to consist of valid lua code and to define the function build(). This function will be called by Modeler 3D and shall return a calculated 3D object.

Base objects are:

cube
cone
cylinder
sphere

Here is a simple example, which creates a cube 10x10x10.

function build() return cube(10); end

Named parameters

A02_Cone

A cone is an object, which is defined by more than one parameter:

The height of the cone
The radius at the base
The radius at the top (optional)
The number of slices to approximate a circle (optional)

Possible invocation for height 10 and base radius 5:

cone(5, 10)

For better clarity, named parameters is recommended to be used:

function build() return cone{radiusTop=1, height=10, radiusBase=5}; end

Part movement

A03_Movement

Any object can be moved, rotated, centered or scaled. Movement can be performed by a vector of x/y/z. Rotation is supported along the x-axis,y-axis and/or z-axis. The angle is given in units of degrees. These movements can be performed on any object.

function build() cy = cylinder{radius=2, height=10}; moved = cy:translate{z=5}; rotated = moved:rotate{ang_x=45}; return rotated; end

CSG Operations

A04_CSG_Operations

By use of Constructive Solid Geometry (CSG) operations, objects can be combined to create all sorts of geometries.

Supported are:

Union
Difference
Xor
Intersection

This examples combines a sphere and a cone

function build() c = cone{radiusBase=0.1, radiusTop= 5, height=10}; s = sphere(5):translate{z=8}; return c + s; end

Sketches

A05_Sketches

For even more flexibility, arbitrary 2D objects can be defined and turned into a 3D object.

2D objects can be defined using:

circle
ellipse
rectangle
square
isogon
text
Sketch() for arbitrary curves
Combinations of sketches with xor

In order to turn any 2D object into an 3D object, the extrude operation can be applied.

function build() s = square(10):translate{x=-5,y=-5}; c = circle{diameter=1}:translate{x = -2}; i = isogon{outer=1, sides=6}:translate{x =2}; sketch = s ^ c ^ i; return sketch:extrude(1); end

Loft

A06_Loft

An even more versatile way to create an 3D object is offered by the Loft feature. This works by connecting sketches placed arbitrarily in the x/y/z-coordinate system

function build() path = { {-2,-2}, {-2, 1}, { 2, 2}, { 1,-2} } s0 = Sketch(path) sketches = {} for i = 0,10 do phi = i * math.pi /10 scale = math.sin(2 * phi) * 0.6 + 1 x = math.cos(2 * phi) y = math.sin(phi) s = s0:translate{x = 0,y = 0,z = 2*i} :scale{x=scale, y=scale, z=1} :rotate{ang_z = 20*(1-x)} :rotate{ang_y = 3*i}; table.insert(sketches,s) end return Mesh.loft(sketches); end

Vectors

A07_Vectors

Vectors are fully supported and can be used for any function, which requires x/y/z-values as parameter

Here is a simple example.

function build() x = vec3(4,0,0) y = vec3(0,4,0) res = x:cross(y) return cube(1):translate(res); end

Quaternions

A08_Quaternions

Further supporting rotation of vectors, quaternions are fully supported, too.

The following example rotates a vector around the z-axes by 90°, which will result in a vector in y-direction.

Important to note: the angle is in radians.

function build() x = vec3(4,0,0) q = quat.fromAngleAxis(math.pi/2, 0, 0, 1) res = x:rotate(q) return cube(1):translate(res); end

Materials/Colors

A09_Materials

For better distinguishing of parts in the assembly view. For a finished part a material aka color can be assigned by a name.

function build() return cube(10):finalize("green"); end

Reference

2D Objects - Circle

R01_2D_Circle

In order to create a 2D circle, there are six possible calls:

circle(r)
circle(r, s)
circle{radius=r}
circle{radius=r,segments=s}
circle{diameter=d}
circle{diameter=d,segments=s}

A circle will be placed in the x/y-plane and centered in the origin. Radius r is the distance from the center to the circle perimeter. The diameter is just double of the radius r. Current implementation tries to achieve a best fit to the radius r. This means, some parts of the approximated circle will be outside and some parts within the ideal circle. The optional value s defines the number of segments, in which a full circle is divided into and then approximated using triangles. This means s=4 will yield a square and s=8 an octagon.

The default for segments is 16.

Minimum number of segments is 3 and its maximum is 1000.

Radius r shall be within the range between 0.001 and 1,000,000

function build() o2d = circle{radius=10, segments=32}; return o2d:extrude(1); end

2D Objects - Ellipse

R02_2D_Ellipse

In order to create a 2D ellipse, there are four possible calls:

ellipse(l, w)
ellipse(l, w, s)
ellipse{length=l, width=w}
ellipse{length=l, width=w, segments=s}

An ellipse will be placed in the x/y-plane and centered in the origin. The length is in x-direction and the width in y-direction. Both values (length and width) are measured from the origin to the crosspoint of ellipse and x/y-axes. Current implementation tries to achieve a best fit. This means, some parts of the approximated ellipse will be outside and some parts within the ideal ellipse. The optional value s defines the number of segments, into which a full circle of 360° is divided into and then approximated by triangles.

The default for segments is 16.

Minimum number of segments is 3 and its maximum is 1000.

Length l and width w shall be within the range between 0.001 and 1,000,000

function build() o2d = ellipse{length=20, width=10, segments=32}; return o2d:extrude(1); end

2D Objects - Square

R03_2D_Square

In order to create a 2D square, there are two possible calls:

square(s)
square{size=s}

A square will be placed in the x/y-plane, with one corner in the origin.

The size s shall be within the range between 0.001 and 1,000,000

function build() o2d = square{size=10}; return o2d:extrude(1); end

2D Objects - Rectangle

R04_2D_Rectangle

In order to create a 2D rectangle, there are two possible calls:

rectangle(l, w)
rectangle{length=l, width=w}

A rectangle will be placed in the x/y-plane, with one corner in the origin. The length is in x-direction and the width in y-direction.

Length l and width w shall be within the range between 0.001 and 1,000,000

function build() o2d = rectangle{length=20, width=10}; return o2d:extrude(1); end

2D Objects - Isogon

R05_2D_Isogon

In order to create a 2D isogon, there are three possible calls:

isogon(o, s)
isogon{outer=l, sides=s}
isogon{perimeter=p, sides=s}

An isogon will be placed in the x/y-plane and centered in the origin. The outer value is the distance from origin to any corner point. An alternative definition uses the perimeter, which is the length of all sides summed up. The number of corners and sides is defined by parameter s.

Minimum number of sides is 3 and its maximum is 1000.

Outer o and perimeter p shall be within the range between 0.001 and 1,000,000

function build() o2d = isogon{outer=10, sides=8}; return o2d:extrude(1); end

2D Objects - Text

R06_2D_Text

In order to create a 2D text, there is one possible call:

text(s)

function build() o2d = text("Hello"); return o2d:extrude(1):rotate{ang_z=180}; end

2D Objects - Path

R07_2D_Path

In order to not be limited to these predefined 2D objects, an arbitrary path consisting of an array of 2D points can be used. Self-intersecting paths are not allowed.

A sketch is created by one of these calls:

Sketch(table)
Sketch{{x,y},....}

table means here a list of {x,y}-pairs.

The below code fills the array path with (x,y) pairs. The function Sketch() takes this path and creates a closed path out of it. The path will be checked to be free of self-intersecting edges.

2D Objects - Union

R08_2D_Xor

Sketches can be combined with xor. Overlaps and sketches within a sketch are allowed.

An xor is defined using the operator for xor:

sketch1 ^ sketch2

So let's extend the previous example, add more shapes, make a xor and see the effect on the resulting solid.

2D Sketch - Translation

R12_2D_Translate

2D Sketches can be moved in the coordinate system to any point.

This translation can be performed selectively along x-, y- and/or z-axes with the displacement vector (dx,dy,dz) or v as vec3:

object:translate(dx,dy,dz)
object:center{x=dx, y=dy, z=dz}
object:translate(v)

If any of the dx,dy,dz components are not given, then the default is 0. If none of the components x,y,z are defined, then this is an error.

If the resulting sketch is moved out of the x-y-plane, then no further Sketches can be combined to it.

The displacements dx,dy,dz shall be within the range -1,000,000 and 1,000,000

function build() s = circle(3):translate{x = 5} return s:extrude(10); end

2D Sketch - Rotation

R13_2D_Rotate

2D Sketches can be rotated in the coordinate system. Rotation axes is always the coordinate system axes !

Rotation can be performed selectively around x-, y- and/or z-axes. The rotation angle is given in degrees (360° full circle):

object:rotate(ax,ay,az)
object:rotate{ang_x=ax, ang_y=ay, ang_z=az}
object:rotate(q)

With q being a quaternion.

If the resulting sketch is moved out of the x-y-plane, then no further Sketches can be combined to it.

If any of the ax,ay,az components are not given, then the default is 0. If none of the components ang_x/y/z are defined, then this is an error.

function build() s = rectangle(4,1):rotate{ang_z = 30} return s:extrude(1); end

2D Sketch - Scale

R14_2D_Scale

2D Sketches can be scaled in size.

Scale can be applied selectively to any of the x-, y- and/or z-components.

object:scale(sx,sy,sz)
object:scale{x=sx, y=sy, z=sz}
object:scale(v)

If any of the sx,sy,sz components are not given, then the default is 1.

The scale values sx,sy,sz shall be within the range >0 and 1,000

function build() s = circle(3):scale{x = 2} return s:extrude(10); end

2D into 3D Objects - Extrude

R21_2Dto3D_Extrude

The extrude operation can turn any 2D sketch into a 3D object. The extrusion takes place into the normal vector of the 2D sketch. Normally this is in direction of the positive z-axes-vector.

Extrude operates on a sketch by any of the following equivalent invocations:

sketch:extrude(h)
sketch:extrude{height=h}
Sketch.extrude(sketch, h)
Sketch.extrude(sketch, {height = h})

Height h shall be within the range between 0.001 and 1,000,000

function build() o2d = circle{radius=10, segments=32}; return o2d:extrude(1); end

2D into 3D Objects - Loft

R22_2Dto3D_Loft

The loft operation offers much higher flexibility. An arbitrary number of sketches can be placed in the x/y/z-space and then will be connected. The algorithm will select points between two spaces based on the relative length of each sketches' path.

If sketches is a table of sketches, then loft will be performed by:

Mesh.loft(sketches)

function build() sketch1 = isogon{outer=10,sides=30} :translate{z=0} sketch2 = isogon{outer= 4,sides=12} :translate{z=10} sketch3 = isogon{outer= 3,sides=8} :translate{z=20} sketch4 = isogon{outer=10,sides=60} :translate{z=30} sketches = {sketch1, sketch2,sketch3,sketch4} return Mesh.loft(sketches) end

Reference

3D Objects - Cube

R41_3D_Cube

In order to create a 3D cube, there are two possible calls:

cube(s)
cube{size=s}

A cube will be placed in the x/y/z-coordinate system with one corner in the origin.

Size s shall be within the range between 0.001 and 1,000,000

function build() o2d = cube(10); return o2d; end

3D Objects - Sphere

R42_3D_Sphere

In order to create a 3D sphere, there are four possible calls:

sphere(r)
sphere(r, s)
sphere{radius=r}
sphere{radius=r,slices=s}

A sphere will be placed in the x/y/z-coordinate system and centered in the origin. Radius r is the distance from the center to the perimeter. Current implementation tries to achieve a best fit to the radius r. This means, some parts of the approximated circle will be outside and some parts within the ideal circle. The optional value s defines the number of slices, in which a full circle of any slice is divided into and used as corner points.

The default for slices is 16.

Minimum number of slices is 3 and its maximum is 100.

Radius r shall be within the range between 0.001 and 1,000,000

function build() o2d = sphere(10); return o2d; end

3D Objects - Cylinder

R43_3D_Cylinder

In order to create a 3D cone, there are four possible calls:

cylinder(r, h)
cylinder(r, h, s)
cylinder{radius=r, height=h}
cylinder{radius=r, height=h, segments=s}

A cylinder will be placed in the x/y/z-coordinate system. The lower circle will be centered in the origin. Radius r is the distance from the center to the perimeter. Current implementation tries to achieve a best fit to the radius r. This means, some parts of the approximated circle will be outside and some parts within the ideal circle. The optional value s defines the number of segments, in which a full circle is divided into and then approximated using triangles. This means s=4 will yield a square and s=8 an octagon.

The default for segments is 16.

Minimum number of segments is 3 and its maximum is 1000.

Radius r and height h shall be within the range between 0.001 and 1,000,000

function build() o2d = cylinder{radius = 5, height = 10}; return o2d; end

3D Objects - Cone

R44_3D_Cone

In order to create a 3D cone, there are six possible calls:

cone(rb, h)
cone(rb, h, s)
cone{radius=rb, height=h}
cone{radius=rb, height=h, segments=s}
cone{radiusBase=rb, radiusTop=rt, height=h}
cone{radiusBase=rb, radiusTop=rt, height=h, segments=s}

A cone will be placed in the x/y/z-coordinate system. rb is the radius of the base, which is placed in the x/y-plane. The optional rt is the radius at the top of the cone. The lower circle will be centered in the origin. Radius rb and rt are the distances from the z-axes to the perimeters. Current implementation tries to achieve a best fit to the radius. This means, some parts of the approximated circle will be outside and some parts within the ideal circle. The optional value s defines the number of segments, in which a full circle is divided into and then approximated using triangles.

The default for segments is 16.

Minimum number of segments is 3 and its maximum is 1000.

Height h, radius rb and rt shall be within the range between 0.001 and 1,000,000

function build() o2d = cone{radiusBase = 8, radiusTop = 4, height = 10}; return o2d; end

Reference

3D Objects - Center

R51_3D_Center

3D Objects can be centered to the origin of the coordinate system. As center of the object, the center of the bounding box (!) of an object is used.

Centering of an object can be performed selectively along x-, y- and/or z-axes:

object:center()
object:center{x=bool, y=bool, z=bool}

where bool is either false or true. If not given, false is assumed

function build() o2d = cube(10); return o2d:center{z = true}; end

3D Objects - Translation

R52_3D_Translate

3D Objects can be moved in the coordinate system to any point.

This translation can be performed selectively along x-, y- and/or z-axes with the displacement vector (dx,dy,dz) or v as vec3:

object:translate(v)
object:translate(dx,dy,dz)
object:center{x=dx, y=dy, z=dz}

If any of the dx,dy,dz components are not given, then the default is 0. If none of the components x,y,z are defined, then this is an error.

The displacements dx,dy,dz shall be within the range -1,000,000 and 1,000,000

function build() o2d = cube(10); return o2d:translate{x = -10, z= 10}; end

3D Objects - Rotation

R53_3D_Rotate

3D Objects can be rotated in the coordinate system. Rotation axes is always the coordinate system axes !

Rotation can be performed selectively around x-, y- and/or z-axes. The rotation angle is given in degrees (360° full circle):

object:rotate(ax,ay,az)
object:rotate{ang_x=ax, ang_y=ay, ang_z=az}
object:rotate(q)

With q being a quaternion.

If any of the ax,ay,az components are not given, then the default is 0. If none of the components ang_x/y/z are defined, then this is an error.

function build() o2d = cube(10); return o2d:rotate{ang_x=30, ang_y=-30}; end

3D Objects - Scale

R54_3D_Scale

3D Objects can be scaled in size.

Scale can be applied selectively to any of the x-, y- and/or z-components.

object:scale(sx,sy,sz)
object:scale{x=sx, y=sy, z=sz}
object:scale(v)

If any of the sx,sy,sz components are not given, then the default is 1.

The scale values sx,sy,sz shall be within the range >0 and 1,000

function build() o2d = cube(10); return o2d:scale{z=3}; end

3D Operations - Union

R61_3D_Union

By use of Constructive Solid Geometry (CSG) operations, objects can be combined to create all sorts of geometries.

The first operation discussed is Union. Union is invoked by one of:

object1 + object2
Mesh.union(object1, object2)
Mesh.union(objecttable)
Mesh.union{object1, object2,...}

This examples combines a sphere and a cone

function build() c = cone{radiusBase=0.1, radiusTop= 5, height=10}; s = sphere(5):translate{z=8}; return Mesh.union{c, s}; end

3D Operations - Intersection

R62_3D_Intersection

Another CSG operation is intersection.

Intersection is invoked by one of:

object1 * object2
Mesh.intersection(object1, object2)
Mesh.intersection(objecttable)
Mesh.intersection{object1, object2,...}

This examples intersects a sphere and a cone

function build() c = cone{radiusBase=0.1, radiusTop= 5, height=10}; s = sphere(5):translate{z=8}; return Mesh.intersection(c, s); end

3D Operations - Subtract

R63_3D_Difference

Subtract can be used to cut away one solid from another.

Subtract is invoked by one of:

object1 - object2
Mesh.subtract(object1, object2)

This examples subtracts a sphere from a cone.

function build() c = cone{radiusBase=0.1, radiusTop= 5, height=10}; s = sphere(5):translate{z=8}; return c - s; end

3D Operations - Xor

R64_3D_Xor

An xor-operation between two objects leaves only those parts of the two objects, which are not intersecting.

Xor is invoked by one of:

object1 ^ object2
Mesh.xor(object1, object2)
Mesh.xor(objecttable)
Mesh.xor{object1, object2,...}

Special care has to be taken for this operation, because xor often would create internal holes inside a solid, which is not supported.

This examples combines a cylinder and a cube, which leaves a hole at the place of the intersection.

function build() c = cube(10); s = cylinder(5,10); return (c ^ s) :rotate{ang_y=40, ang_x=-45}; end

Materials/Colors

R71_Materials

A material/color can be assigned, by invoking the finalize() method on a selected mesh. This will yield a finished part to be returned by build()

The current material/color support are for these names:

brown
red
cyan
gray
magenta
white
teal
green
indigo
orange
purple
lightgray
darkgray
blue
yellow
black

function build() return cube(10):finalize("red"); end

Reference

3D Objects and 2D Sketch - Pocket

R81_3D_Pocket

A useful tool to poke arbitrary holes into a 3D object is Pocket. In addition it can be used to emboss e.g. short text into an object.

In order to apply pocket, there are two possible calls:

object:pocket(s,d)
object:pocket(s,{depth=d})

The sketch s needs to be placed on the surface or above the object and pocket will then drill down to depth d

Depth d shall be within the range between 0.001 and 1,000,000

function build() o2d = cube(5):scale{x=8,y=5}; sketch = text("Hello"):translate{x=3,y=3,z=5}; return o2d:pocket(sketch,0.5); end

Vectors

R91_Vectors

All supported vector operations are listed below.

Creation:

v = vec3(x,y,z)

Scalar and Vector arithmetics:

a * v
v / a

Vector arithmetics:

Negate: -v
Length: #v

Componentwise arithemtics

v1 + v2
v1 - v2
v1 * v2
v1 / v2

Functions on vectors:

v:scale(s)
v:length()
v:normalize()
v1:distance(v2)
v1:angle(v2)
v1:dot(v2)
v1:cross(v2)

Interpolation between vector v1 and v2:

v1:lerp(v2,t)

Rotation with a quaternion:

v:rotate(q)
q * v

Examples using print() for output

function build() v1 = vec3(1,0,1) v2 = vec3(0,1,1) print("v1=",v1) print("v2=",v1) print("v1+v2=",v1+v2) print("v1*v2=",v1*v2) print("v1-v2=",v1-v2) print("length(v1)=",v1:length()) print("length(v2)=",v2:length()) print("dot(v1,v2)=",v1:dot(v2)) print("cross(v1,v2)=",v1:cross(v2)) return cube(1):translate(v1); end

Quaternions

R92_Quaternions

Quaternions are used to rotate vectors. In order to obtain quaternions, the following functions are supported:

Important to note: radians is in use.

Creation:

quat(x, y, z, w)
quat.fromAngleAxis(angle, x, y, z)
quat.between(v1, v2)
quat.fromDirection(x, y, z)

Componentwise arithmetics

q1 + q2
q1 - q2
q1 * q2

Quaternion arithmetics

q:scale(s)
q * v
q1 * q2
Negate: -q
Length: #q
q:normalize()

Interpolation between quaternion q1 and q2:

q1:lerp(q2,t)
q1:slerp(q2,t)

Info about quaternion:

q:getAngleAxis()
q:length()

In the following example a cube is rotated in such a way, that the cube's diagonal is pointing in direction of z-axes.

function build() diagonal = vec3(1,1,1):normalize() z_direction = vec3(0,0,1) q = quat.between(diagonal, z_direction) return cube(2):rotate(q); end

Expert Examples

Threaded Rod

X01_Threaded_Rod

The code below calculates the profile of a threaded rod as sketch. Then stacks up this profile elevated and rotated. Finally performs a loft-operation, which is pretty fast.

turns = 10 slices = 30 -- This is the profile of one turn in z-direction function heightAt(ratio,minHeight,deltaHeight) if ratio < 0.25 then return minHeight end ratio = ratio - 0.25 if ratio < 0.3125 then return minHeight+deltaHeight*ratio/0.3125 end ratio = ratio - 0.3125 if ratio < 0.125 then return minHeight+deltaHeight end ratio = ratio - 0.125 return minHeight + deltaHeight*(1-ratio/0.3125) end -- Translate the height profile along the axis into an angular height profile function profile(pitch) pitch = 1 height = 0.541266 * pitch innerDiameter = 3 points = {} for i = 0,slices-1 do ratio = i/slices phi = 2*math.pi*ratio h = heightAt(ratio, innerDiameter, height) x = h * math.cos( phi) y = h * math.sin(-phi) table.insert(points,{x,y}) end return Sketch(points) end function build() pitch = 1 -- Calculate the profile dz = pitch/slices dang = 360/slices p = profile(pitch) -- Stack up the profile s = {} for turns = 2,slices*turns do table.insert(s,p) p = p:translate{z=dz}:rotate{ang_z=dang} end return Mesh.loft(s); end

Involute Gear

X02_Gear

Based on https://github.com/jscad/OpenJSCAD.org/blob/master/packages/examples/parameters/gear.js and translated to Lua by Vicinity International GmbH The MIT License (MIT) Copyright (c) 2017-2021 JSCAD Organization Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

NEMA 17

X03_NEMA17

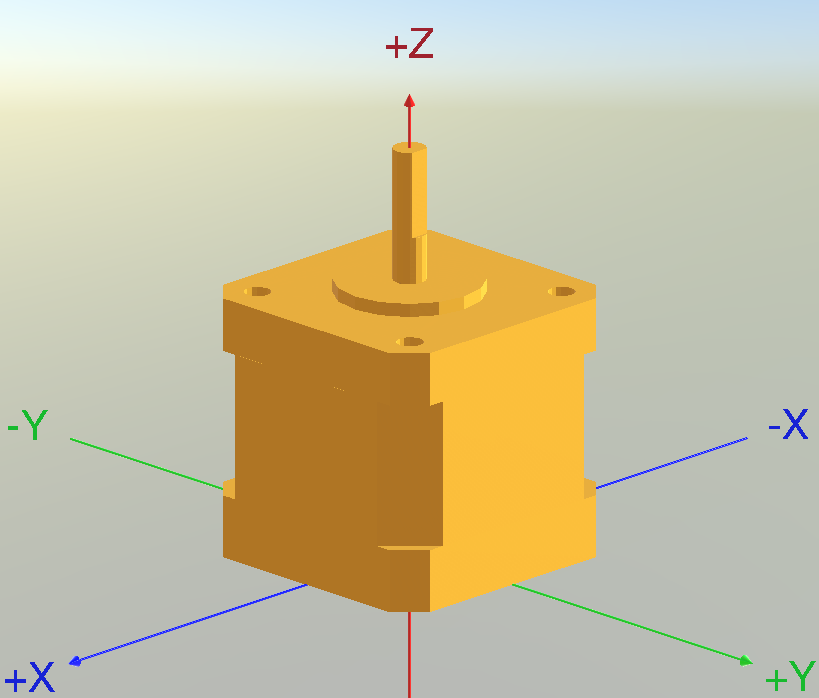
The NEMA17's base is quadratic and can be defined by two dimensions (ignoring the chamfers). One measurement is diagonal from "/" to "/" (or "\" to "\") and the other just the width.

function octagon(diagonal, width) -- 2 -- /-----------\ -- / \ 1 -- | | -- | | -- | | -- | | -- | | -- \ / -- \-----------/ -- Corner point 1 is x=width/2, y=c -- Corner point 2 is x=c, y=width/2 -- To be calculated is c -- The diagonal point is the mean of points 1 and 2: -- x = y = width/4 + c/2 -- Based on this the diagonal is -- d = 2 * sqrt(2) * (width/4 + c/2) -- Given the diagonal c can be determined -- c = (d / (2 * sqrt(2)) - width/4) * 2 -- = d / sqrt(2) - width/2 b = width / 2 c = diagonal / math.sqrt(2) - width / 2 return Sketch({ { b, c}, { c, b}, {-c, b}, {-b, c}, {-b,-c}, {-c,-b}, { c,-b}, { b,-c}, }) end function build_body() diagonal_base = 53.77 width_base = 42.15 height_base = 9.46 s1 = octagon(diagonal_base, width_base) s2 = s1:translate{z = height_base} diagonal_middle = 50.2 width_middle = 42.2 height_middle = 22.10 s3 = octagon(diagonal_middle, width_middle):translate{z = height_base} s4 = s3:translate{z = height_middle} diagonal_top = 53.77 width_top = 42.15 height_top = 8.0 s5 = octagon(diagonal_top, width_top):translate{z = height_base+height_middle} s6 = s5:translate{z = height_top} return height_base + height_middle + height_top, Mesh.loft{s1,s2,s3,s4,s5,s6} end function holes_sketch() hole = circle{diameter = 4}:translate{x = 31/2, y = 31/2} holes = hole ^ hole:rotate{ang_z = 90} holes = holes ^ hole:rotate{ang_z = 180} holes = holes ^ hole:rotate{ang_z = 270} return holes end function build_ring() c = circle{diameter = 22} return 2, c:extrude{height = 2} end function build_axle() c = circle{radius = 5/2} a = c:extrude{height = 20} cutout = rectangle{width = 5, length = 5} :extrude{height = 20} :translate{x = -2.5, y = 2, z = 7} return 20, a:subtract(cutout) end function build() body_height,body = build_body() holes = holes_sketch():translate{z = body_height} body = body:pocket(holes,{depth = 4.5}) ring_height,ring = build_ring() axle_height,axle = build_axle() return Mesh.union{body,ring:translate{z = body_height},axle:translate{z = body_height + ring_height}} end

Screw

X04_Screw

turns = 10 slices = 20 pitch = 1 innerDiameter = 3 height = 0.541266 * pitch screwHeadRadius = 5 screwHeadHeight = 3 hexagonRadius = 3 hexagonDepth = 3 -- This is the profile of one turn in z-direction function heightAt(ratio,minHeight,deltaHeight) if ratio < 0.25 then return minHeight end ratio = ratio - 0.25 if ratio < 0.3125 then return minHeight+deltaHeight*ratio/0.3125 end ratio = ratio - 0.3125 if ratio < 0.125 then return minHeight+deltaHeight end ratio = ratio - 0.125 return minHeight + deltaHeight*(1-ratio/0.3125) end -- Translate the height profile along the axis into an angular height profile function profile(j) points = {} for i = 0, slices-1 do ratio = i/slices phi = 2*math.pi*i/slices ix = i+j-slices f = 1 if ix < slices then f = ix/slices end h = heightAt(ratio, innerDiameter, height*f) x = h * math.cos(phi) y = h * math.sin(phi) table.insert(points,{x,y}) end return Sketch(points) end function build() s = {} -- Calculate the profile dz = pitch/slices dang = 360/slices for j = 1,2*slices do p = profile(j) :rotate{ang_z=dang*j} :translate{z=dz*j} table.insert(s,p) end -- Stack up the profile for turns = slices*2,slices*turns do p = p:translate{z=dz}:rotate{ang_z=dang} table.insert(s,p) end head = isogon(screwHeadRadius,6) :translate{z=slices*turns*dz} table.insert(s,head) table.insert(s, head:translate{z=screwHeadHeight}) hexagon = isogon(hexagonRadius,6) :translate{z=slices*turns*dz + screwHeadHeight} table.insert(s, hexagon) table.insert(s, hexagon:translate{z=-hexagonDepth}) m = Mesh.loft(s); return m end